Algebra and calculus

Calculus

Calculus helps us to understand the gradient of a curve.

Gradient function

The derivative gives us a ‘gradient function’ i.e. a formula that will give the gradient at a point on the curve.

The gradient on a curve is different at different points on a curve.

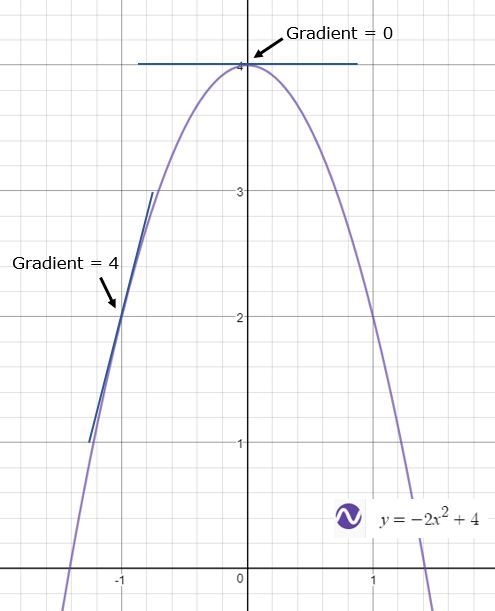
On this graph:

When $x < 0$ the gradient is positive.

When $x = 0$ the gradient is equal to zero.

When $x > 0$ the gradient is negative.

Differentiation

To find the gradient function (derivative) for a model or graph we differentiate the function. The technique of differentiation can be carried out using algebraic manipulation.

Find out more about algebraic manipulation such as rearranging equations and the law of indices.

In general : For the function $y = ax^{n}$ then $\frac{dy}{dx} = nax^{n-1}$

Khan academy step though this power rule with a number of examples.

e.g.

$y = 3x^{3}$ then $\frac{dy}{dx} = 9x^{2}$

The following video will take you through three more examples of differentiation of a polynomial.

Practice this technique on Khan Academy. Hints and further videos are available.

Notation

There are three commonly used notation methods for the derivative of a function.

If $x^{2}$ then $\frac{dy}{dx} = 2x$	$\frac{dy}{dx}$ is the derivative of $y$ with respect to $x$
If $f(x) = x^{2}$ then $f'(x) = 2x$	$f'(x)$ is the gradient function of $f(x)$
$\frac{d}{dx} (x^{2}) = 2x$	If we differentiate $x^{2}$ with respect to $x$ we get $2x$

Learning Hub

Learning Hub team
Workshops
Drop in booth
Learning leaders
Pass Leaders
Business library guides

Life on campus
Careers centre
Student support
He Tuākana
AskAuckland student centre